Short Notes on Bayesian Inference of Vector Autoregressive Models
with tags r bayes var rcpp armadillo -During the past years I realised that econometric analyis can be understood as a craft. You learn your basics at school from more or less motivated/talented professors and then you are sent out into wild, where you are confronted with real life challenges that differ from the stylised exmples you have become used to during your studies. This comes with a bunch new insights that I want to document on this page. It should become a collection of notes on Bayesian VAR modelling that have become imporant to me over the last years.
Prior specification
General issues
The prior precision matrix is the inverse of the variance matrix. In Bayesian econometrics it is common to work with the precision matrix, since it is mathematically more convenient. Apart from algrebraic considerations you can express an uninformative prior by setting the respective value to zero. Otherwise you would have to work with infinite values, which is…well…just not good.
Be aware of potentially high mean values of intercepts. If you work with time series data, which fluctuates aroung a mean of 100, this should be reflected in the priors of the intercept terms. You might wish to change the prior mean to the mean of the series. Or you could set it to the first value, if you add a deterministic trend term as well.
Be aware of the scales of your errors. The prior variance of the error term should be reasonably proportional to the scale of the data. For example, when working with log-differenced growth rates of macroeconomic time series an increase of 1 percent is indicated by the value 0.01. However, a lot of economic data comes in a format, where 1 percent is indicated by a value of 1. Change the priors of your error terms accordingly!
Don’t use too large priors for SSVS and BVS. This might lead to a situation, where the algorithm cannot jump back to a state, where a certain variable should not be included in the model. See George et al. (2008) and Korobilis (2013).
Obtain (much) more draws from the posteriors than usual when using SSVS or BVS. This helps if the inclusion parameters tend to change very rarely.
Common prior specifications for time series models
| Variables | Prior | Source |
|---|---|---|
| Non deterministic coefficients | N(0,IM) | Chan et al. (2019) |
| Intercepts for stationary data with zero mean | N(0,10IN) | Chan et al. (2019) |
| Covariance matrix | IW(df=K+3,scale=IK) | Chan et al. (2019) |
| Variances | IG(shape=0.01,rate=0.01) | Chan et al. (2019), George et al. (2008) |
| Inclusion probabilities | 0.5 | Chan et al. (2019), George et al. (2008), Korobilis (2013) |
K is the number of endogenous variables. M is the number of non-deterministic regressors and N is the number of intercept terms.
Computational issues
Distribututions
Gamma distribution
Be aware that the gamma distribution has can be described by different parameterizations. Either use shape and scale or shape and rate. Sometimes the mean and variance of the distribution are provided.
The Wishart and gamma distributions are related.
prior_df <- 100
prior_var <- 10
n <- 10000# Draw from Wishart distribution
set.seed(1)# Reset random number generator
wish <- 1 / rWishart(n, df = prior_df, Sigma = diag(1 / prior_var, 1))[1, 1, ]
hist(wish, main = "IW(100 ,10)", xlab = NULL)
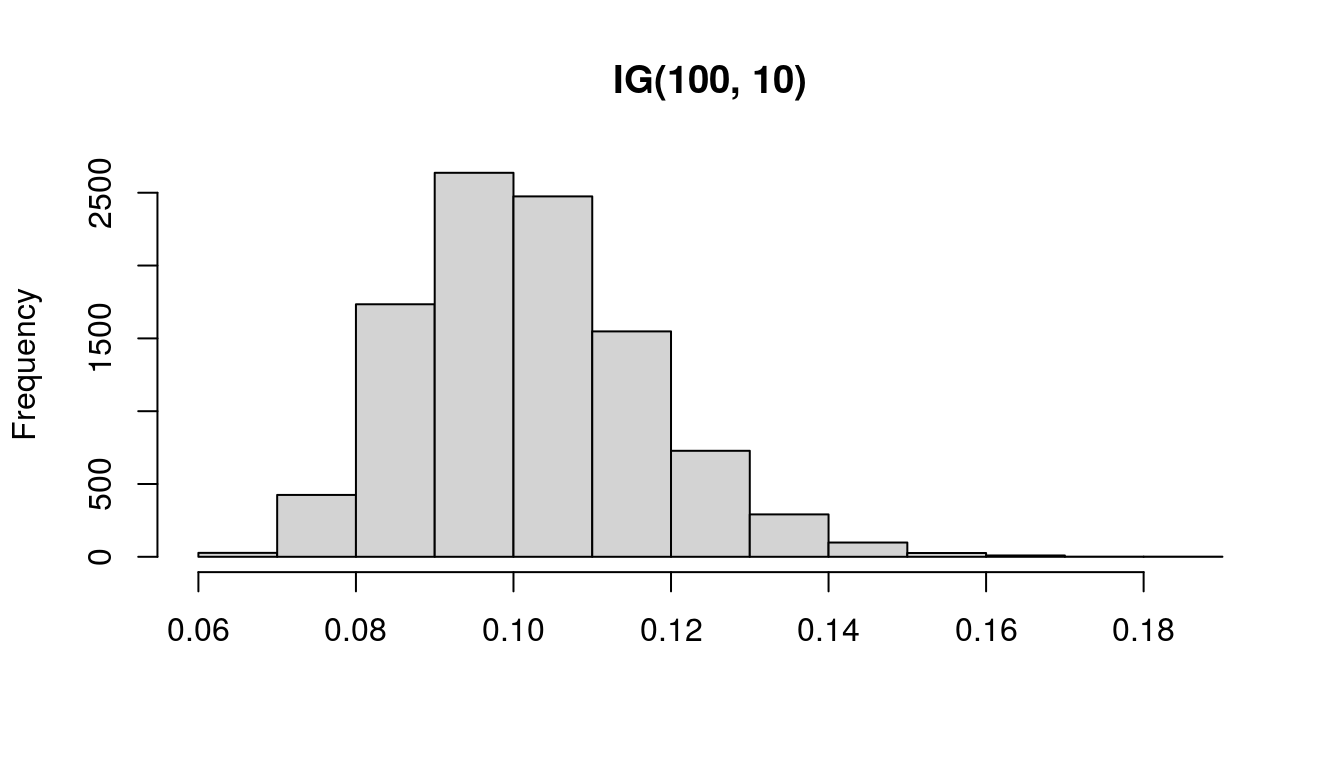
# Draw from Gamma distribution
set.seed(1) # Reset random number generator
gamm <- 1 / rgamma(n, shape = prior_df / 2, scale = 1 / (prior_var / 2))
hist(gamm, main = "IG(100, 10)", xlab = NULL)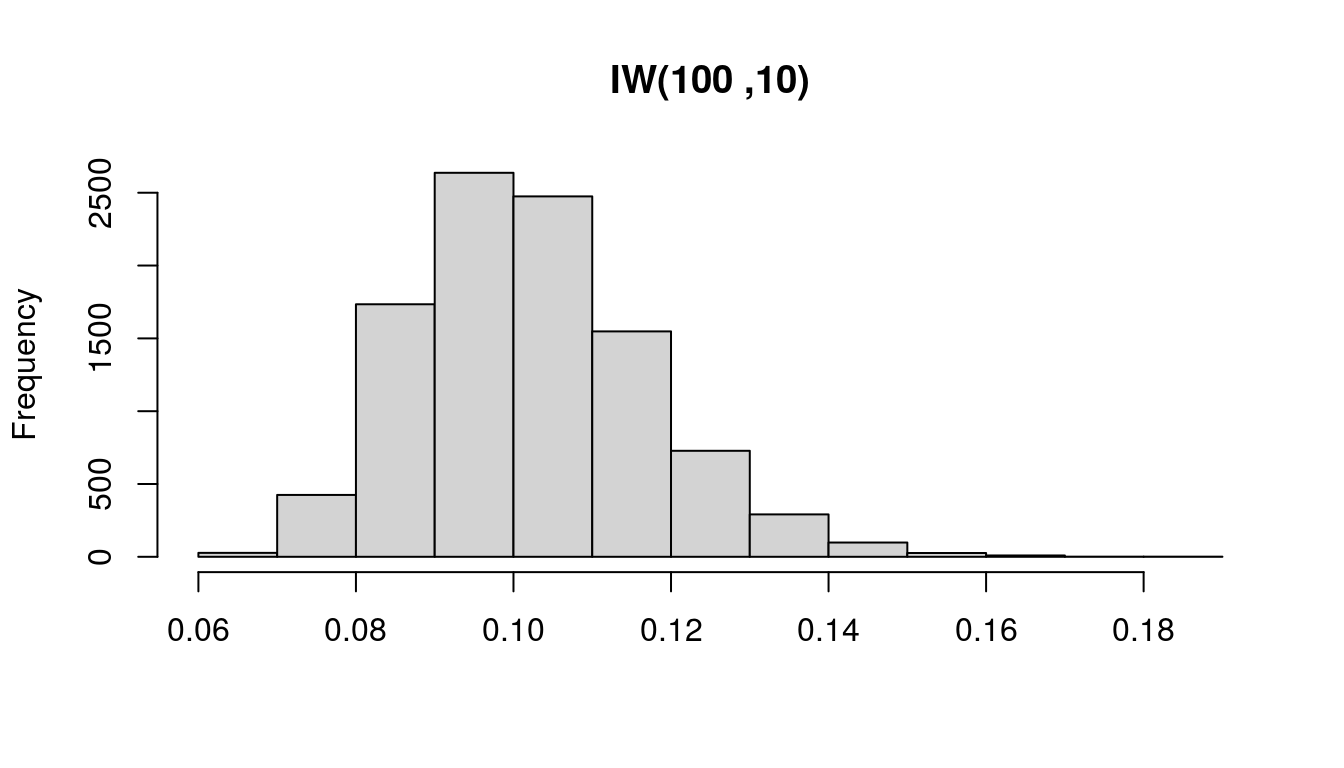
Sparse matrices
- Avoid switching between sparse and dense matrices.
Using RcppArmadillo
Consider programming loops in C++. It’s way faster! Or change the programming language.
Do everthing either in R or in C++, if you use sparse matrices.
References
Chan, J., Koop, G., Poirier, D. J., & Tobias J. L. (2019). Bayesian econometric methods (2nd ed.). Cambridge: Cambridge University Press.
George, E. I., Sun, D., & Ni, S. (2008). Bayesian stochastic search for VAR model restrictions. Journal of Econometrics, 142(1), 553-580. https://doi.org/10.1016/j.jeconom.2007.08.017
Koop, G., & Korobilis, D. (2010). Bayesian multivariate time series methods for empirical macroeconomics. Foundations and trends in econometrics, 3(4), 267-358. https://dx.doi.org/10.1561/0800000013
Korobilis, D. (2013). VAR forecasting using Bayesian variable selection. Journal of Applied Econometrics, 28(2), 204-230.