Bayesian Error Correction Models with Priors on the Cointegration Space
with tags r bvec vec cointegration bvartoolsIntroduction
This post provides the code to set up and estimate a basic Bayesian vector error correction (BVEC) model with the bvartools package. The presented Gibbs sampler is based on the approach of Koop et al. (2010), who propose a prior on the cointegration space.
Data
To illustrate the estimation process, the dataset E6 from Lütkepohl (2007) is used, which contains data on German long-term interest rates and inflation from 1972Q2 to 1998Q4.
library("bvartools")
data("e6")
plot(e6) # Plot the series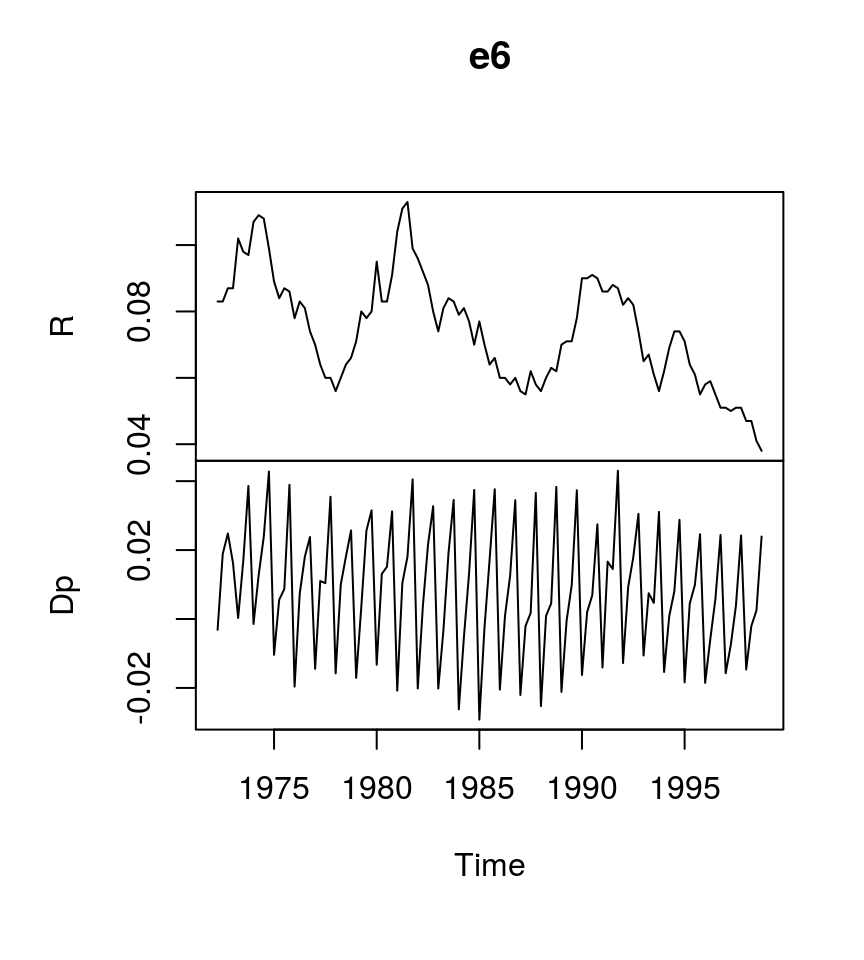
The create_bvecmodel function produces an object of class bvecmodel, whose element data$train contains the inputs y, w and x for the BVEC estimator, where y is the matrix of dependent variables, w is a matrix of potentially cointegrated regressors, and x is the matrix of non-cointegration regressors. The matrices contain one row per period. Since the sampler below is written for matrices with one column per period, they are transposed.
model <- create_bvecmodel(e6,
p = 4,
r = 1,
const = "unrestricted",
seasonal = "unrestricted")
y <- t(model[["data"]][["train"]][["y"]])
w <- t(model[["data"]][["train"]][["w"]])
x <- t(model[["data"]][["train"]][["x"]])Estimation
# Reset random number generator for reproducibility
set.seed(7654321)
iter <- 10000 # Number of iterations of the Gibbs sampler
burnin <- 5000 # Number of burn-in draws
store <- iter - burnin
r <- 1 # Set rank
tt <- ncol(y) # Number of observations
k <- nrow(y) # Number of endogenous variables
k_w <- nrow(w) # Number of regressors in error correction term
# Number of differenced regressors and unrestricted deterministic terms
k_x <- nrow(x)
k_alpha <- k * r # Number of elements in alpha
k_beta <- k_w * r # Number of elements in beta
k_gamma <- k * k_x
# Set uninformative priors
# ...for loadings and non-cointegration parameters
# Vector of prior parameter means
a_mu_prior <- matrix(0, k_alpha + k_gamma)
# Inverse of the prior covariance matrix
a_v_i_prior <- diag(0, k_alpha + k_gamma)
# ...for cointegration parameters
v_i <- 0
p_tau_i <- matrix(0, k_w, k_w)
p_tau_i[1:r, 1:r] <- diag(1, r)
#...for the error term
u_sigma_df_prior <- r # Prior degrees of freedom
u_sigma_scale_prior <- diag(0, k) # Prior covariance matrix
u_sigma_df_post <- tt + u_sigma_df_prior # Posterior degrees of freedom
# Initial values
beta_draw <- matrix(c(1, -4), k_w, r)
u_sigma_i <- diag(.0001, k)
u_sigma <- solve(u_sigma_i)
g_i <- u_sigma_i
# Data containers
draws_alpha <- matrix(NA, k_alpha, store)
draws_beta <- matrix(NA, k_beta, store)
draws_pi <- matrix(NA, k * k_w, store)
draws_gamma <- matrix(NA, k_gamma, store)
draws_sigma <- matrix(NA, k^2, store)
# Start Gibbs sampler
for (draw in 1:iter) {
# Draw conditional mean parameters
temp <- post_coint_kls(y = y,
beta = beta_draw,
w = w,
x = x,
sigma_i = u_sigma_i,
v_i = v_i,
p_tau_i = p_tau_i,
g_i = g_i,
gamma_mu_prior = a_mu_prior,
gamma_v_i_prior = a_v_i_prior)
alpha_draw <- temp[["alpha"]]
beta_draw <- temp[["beta"]]
pi_draw <- temp[["Pi"]]
gamma_draw <- temp[["Gamma"]]
# Draw variance-covariance matrix
u <- y - pi_draw %*% w - matrix(gamma_draw, k) %*% x
beta_p_beta <- crossprod(beta_draw, p_tau_i) %*% beta_draw
alpha_prior <- v_i * alpha_draw %*% tcrossprod(beta_p_beta, alpha_draw)
u_sigma_scale_post <- solve(tcrossprod(u) + alpha_prior)
u_sigma_i <- rWishart(1, u_sigma_df_post, u_sigma_scale_post)[, , 1]
u_sigma_i <- matrix(u_sigma_i, k)
u_sigma <- solve(u_sigma_i)
# Update g_i
g_i <- u_sigma_i
# Store draws
if (draw > burnin) {
draws_alpha[, draw - burnin] <- alpha_draw
draws_beta[, draw - burnin] <- beta_draw
draws_pi[, draw - burnin] <- pi_draw
draws_gamma[, draw - burnin] <- gamma_draw
draws_sigma[, draw - burnin] <- u_sigma
}
}Obtain point estimates as the mean of the parameter draws:
gamma_mean <- rowMeans(draws_gamma) # Obtain means for every row
gamma_mean <- matrix(gamma_mean, k) # Transform mean vector into a matrix
gamma_mean <- round(gamma_mean, 3) # Round values
# Rename matrix dimensions
dimnames(gamma_mean) <- list(dimnames(y)[[1]], dimnames(x)[[1]])
round(gamma_mean, 3) # Print## d.R.l01 d.Dp.l01 d.R.l02 d.Dp.l02 d.R.l03 d.Dp.l03 const season.1 season.2 season.3
## d.R 0.267 -0.187 -0.017 -0.207 0.225 -0.099 0.002 0.001 0.009 0.000
## d.Dp 0.074 -0.383 0.000 -0.421 0.025 -0.361 0.011 -0.034 -0.018 -0.017# Obtain means for every row
beta_mean <- rowMeans(t(t(draws_beta) / t(draws_beta)[, 1]))
beta_mean <- matrix(beta_mean, k_w) # Transform mean vector into a matrix
beta_mean <- round(beta_mean, 3) # Round values
dimnames(beta_mean) <- list(dimnames(w)[[1]], NULL) # Rename matrix dimensions
beta_mean # Print## [,1]
## l.R 1.000
## l.Dp -3.969sigma_mean <- rowMeans(draws_sigma) # Obtain means for every row
sigma_mean <- matrix(sigma_mean, k) # Transform mean vector into a matrix
sigma_mean <- round(sigma_mean * 10^4, 2) # Round values
# Rename matrix dimensions
dimnames(sigma_mean) <- list(dimnames(y)[[1]], dimnames(y)[[1]])
sigma_mean # Print## d.R d.Dp
## d.R 0.29 -0.02
## d.Dp -0.02 0.27bvec objects
The bvec function can be used to collect output of the Gibbs sampler in a standardised object, which can be used further for forecasting, impulse response analysis or forecast error variance decomposition.
# Number of non-deterministic coefficients
k_nondet <- (k_x - 4) * k
# Generate bvec object
bvec_est <- bvec(y = model[["data"]][["train"]][["y"]],
w = model[["data"]][["train"]][["w"]],
x = model[["data"]][["train"]][["x"]][, 1:6],
x_d = model[["data"]][["train"]][["x"]][, 7:10],
r = 1,
alpha = draws_alpha,
beta = draws_beta,
Gamma = draws_gamma[1:k_nondet, ],
C = draws_gamma[(k_nondet + 1):nrow(draws_gamma), ],
Sigma = draws_sigma)The error correction term is described by the draws of alpha and beta and not by those of Pi, since the latter cannot be decomposed into the former.
Posterior draws can be thinned with function thin:
bvec_est <- thin(bvec_est, thin = 5)The function vec_to_var can be used to transform the VEC model into a VAR in levels:
bvar_form <- vec_to_var(bvec_est)Forecasts
Forecasts are obtained in two steps. First, function add_forecast_input generates the data of the forecast periods. Values of deterministic terms such as the seasonal dummies can be provided in its argument deterministic. If they are not provided, the function tries to obtain them from the model. Second, function add_posterior_forecasts simulates the forecasts.
bvar_form <- add_forecast_input(bvar_form, n_ahead = 10)
bvar_form <- add_posterior_forecasts(bvar_form)
bvar_pred <- predict(bvar_form, n_ahead = 10)
plot(bvar_pred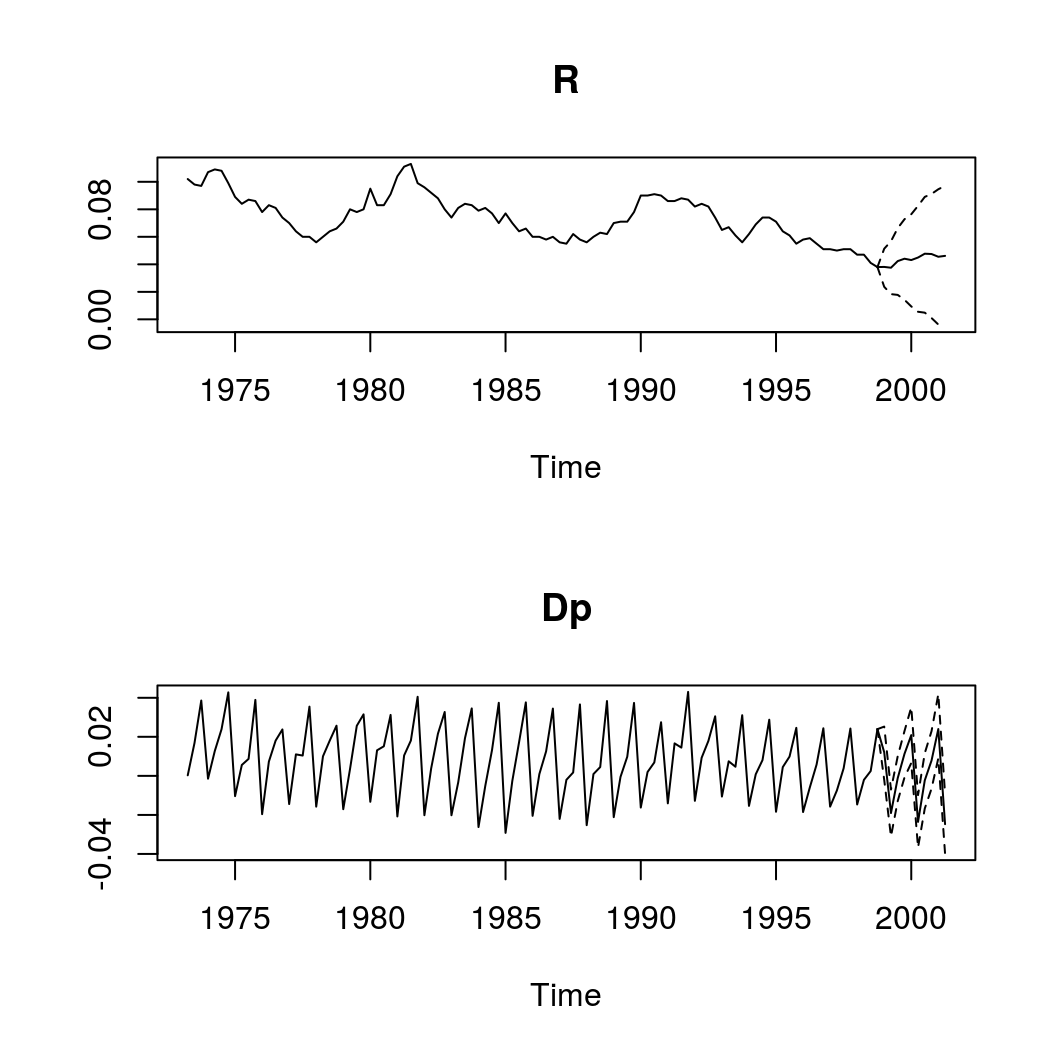, n_pre = 20)
Impulse response analysis
Impulse responses for VECs can be constructed from their VAR respresentations.
ir <- irf(bvar_form, impulse = "R", response = "Dp", n_ahead = 20)
plot(ir,
main = "Forecast Error Impulse Response",
xlab = "Year",
ylab = "Response")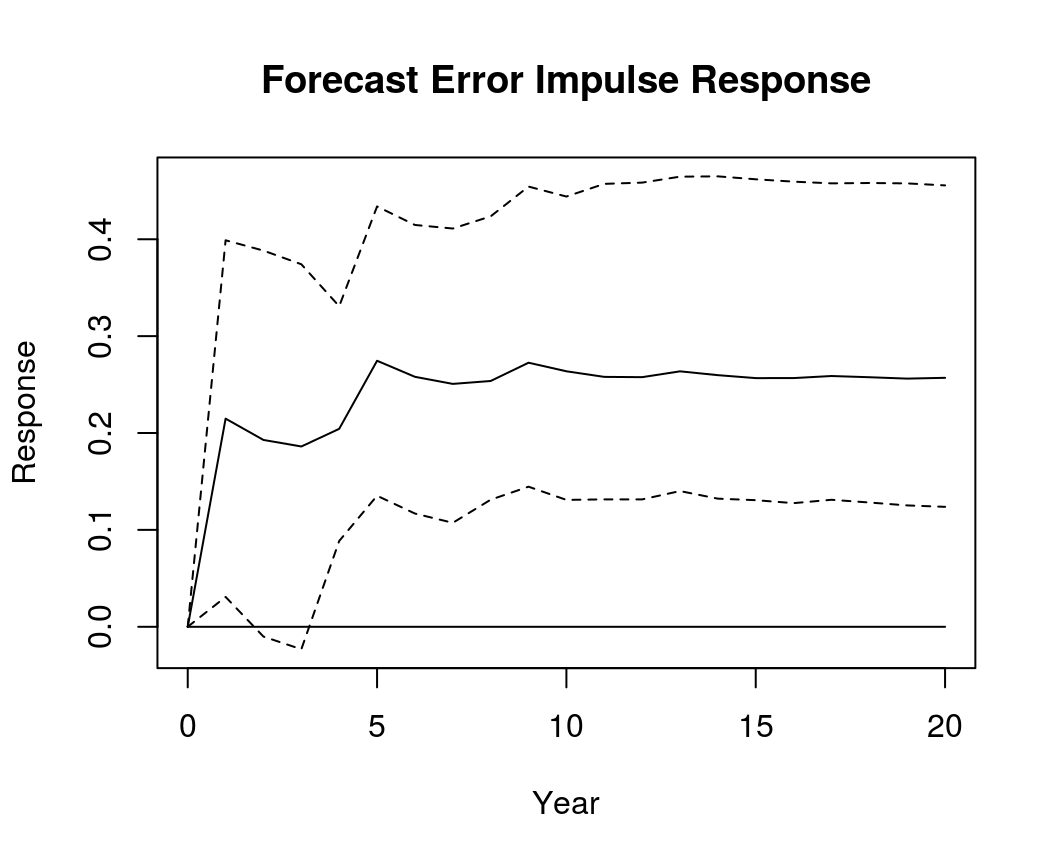
Orthogonalised impulse response
oir <- irf(bvar_form,
impulse = "R",
response = "Dp",
n_ahead = 20,
type = "oir")
plot(oir,
main = "Orthogonalised Impulse Response",
xlab = "Year",
ylab = "Response")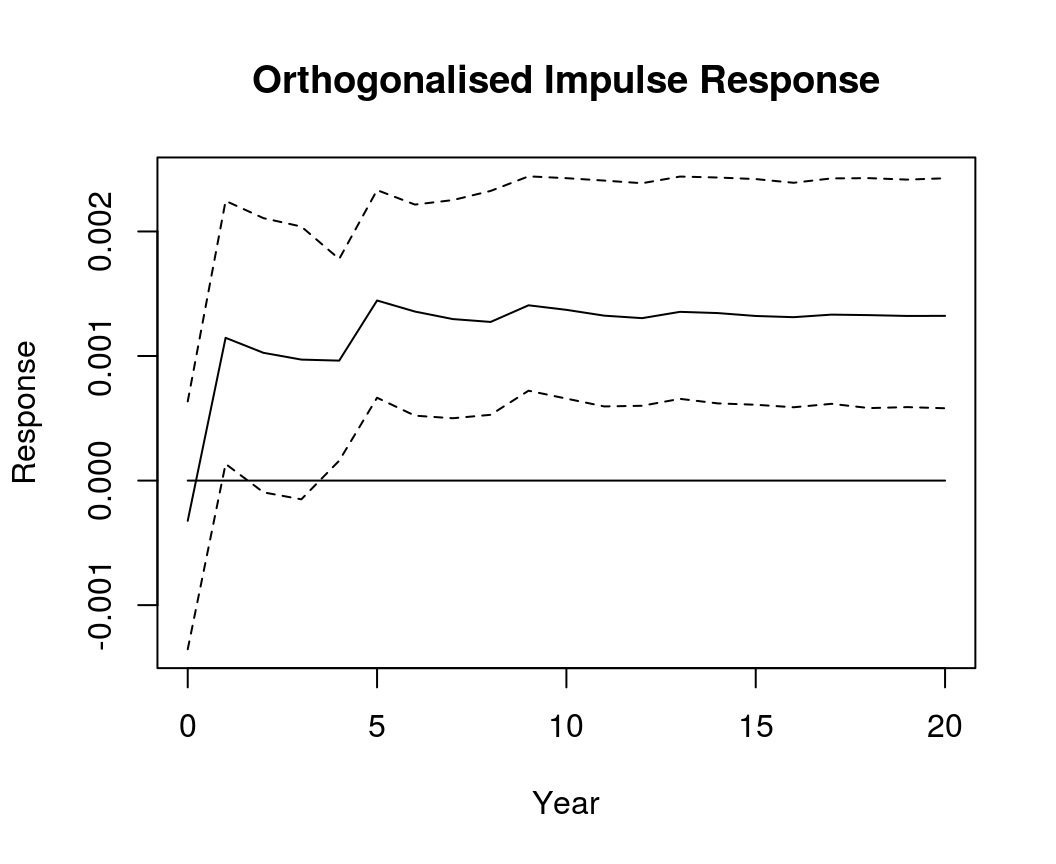
Generalised impulse response
gir <- irf(bvar_form,
impulse = "R",
response = "Dp",
n_ahead = 20,
type = "gir")
plot(gir,
main = "Generalised Impulse Response",
xlab = "Year",
ylab = "Response")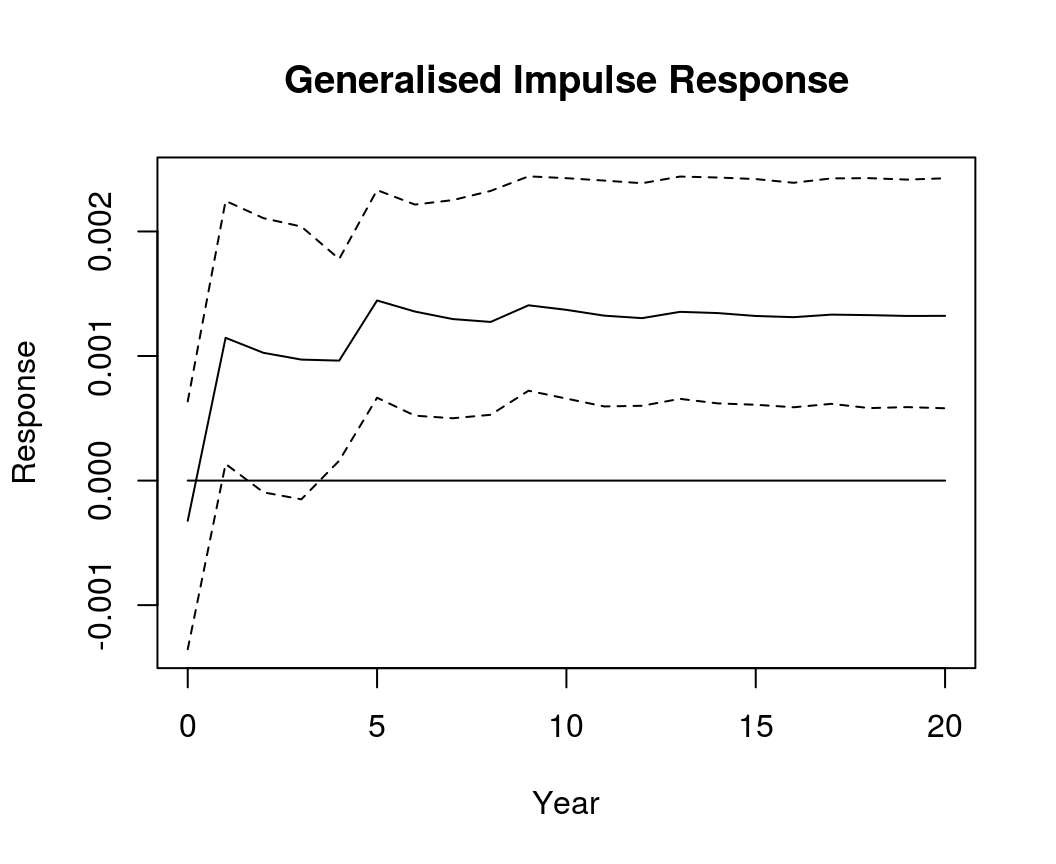
Forecast error variance decomposition
bvec_fevd <- fevd(bvar_form, response = "Dp", n_ahead = 20)
plot(bvec_fevd, main = "FEVD of inflation")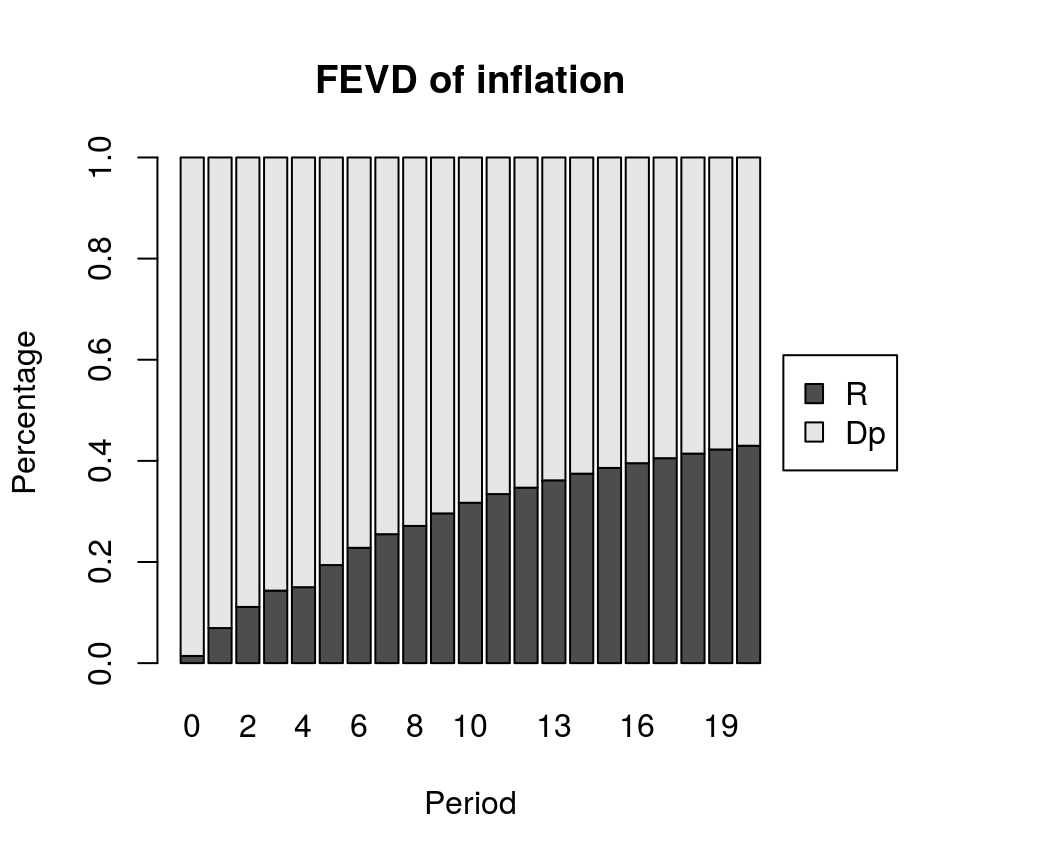
References
Koop, G., León-González, R., & Strachan R. W. (2010). Efficient posterior simulation for cointegrated models with priors on the cointegration space. Econometric Reviews, 29(2), 224-242. https://doi.org/10.1080/07474930903382208
Lütkepohl, H. (2007). New introduction to multiple time series analysis (2nd ed.). Berlin: Springer.
Pesaran, H. H., & Shin, Y. (1998). Generalized impulse response analysis in linear multivariate models, Economics Letters, 58, 17-29. https://doi.org/10.1016/S0165-1765(97)00214-0
